IN-FLIGHT ANALISYS of the YOHKOH PSF FUNCTION

S. Gburek end J.Sylwester

Abstract

Instrumental blurring is one of the main factors which affects quality of telescopic images. Blurring causes problems with interpretation of recorded images, obscures morphology of observed structures and spoils photometric precision. Several methods, called commonly deconvolution methods, (ANDRIL, MEM IRIS, LUCY, PIXON, etc.) have been invented specifically for the purpose of deblurring astronomical images. Majority of these methods assume a priori knowledge of the physical instrument response to a point source which is described by point spread function (PSF). Hence, the question of determining PSF becomes critical. We show a novel method of recovering in-flight PSF of satellite-born telescopes directly from the measured images. Presented method is especially useful for solar instruments as it works with the (non point-like) extended sources. One of the rare opportunities for the investigation of the shape of the PSF is the use of solar eclipses. There were several of them seen by Yohkoh. However only some have had the importance on the subject. The essence of the presented method consists in realising that the shape of PSF is certainly going along the steepest slopes present in the data. In respect to this we have performed the analysis of selected images where the recovery of the PSF has been well defined. Our starting concept was to look into the SXT patterns where substantial coverage of the intensity measurements was available and the sources looked confined.

Key words: psf; eclipses; sxt; yohkoh

INTRODUCTION

Astronomical imaging instruments, such as ground-based or space-born telescopes, generally smear the information about an observed object. By making the observation, any image may be considerably degraded due to the noise, blurring and other instrumental factors. In case of imaging, one of the most widely used mathematical models of image formation process is based on the notion of a point spread function - PSF. Such a function describes the way in which a single point source is imaged (represented) by the instrument. In the model, a measured image arises as a convolution of the real object brightness distribution and the PSF. Additional ambiguity is introduced due to photon shot noise. A variety of image deconvolution algorithms have been suggested in order to recover the true brightness distributions from the observed images. Many of these algorithms rely on the mentioned model of image formation and therefore assume the prior knowledge of PSF function. The exception, is the blind deconvolution approach in which both brightness distribution and PSF are determined simultaneously within self-consistent iterative process. However, a good approximation of the PSF can significantly improve the blind deconvolution algorithm performance.

The determination of the PSF for the image restoration purposes is essential. Existing methods give mostly unsatisfactory results for the instruments being placed in orbit. Empirical calibration tests allow measuring the PSF shape within accessible laboratory circumstances. However, the PSF may change during the instrument lifetime and needs to be recalibrated; this is often impracticable, particularly for the satellite onboard telescopes. Analytical methods that attempt to describe the PSF shape using analytical formulae usually yield a good estimation of the PSF shape, but it is hard to handle smaller structural PSF features in this approach. Moreover formal approximations are dependent on details of the specific calibration method. There are also methods to regain PSF shape directly from the recorded images. These are capable of providing less vulnerable shape of PSF than the analytical ones and can be applied on line. Presented method belongs to the last category. This method and its application for Yohkoh SXT images telescope is discussed in the sequel.

YOHKOH SXT POINT SPREAD FUNCTION

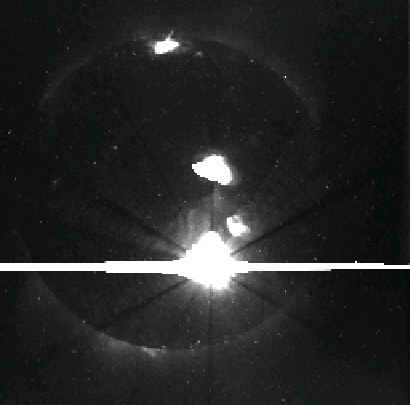
The Yohkoh satellite was launched from Kagoshima Space Center on August 31, 1991. The goal of its mission is to observe solar radiation in X-ray and g-ray energy spectrum. The Soft X-ray telescope (SXT) is one of the X-ray instruments in use aboard the satellite. It has been developed by USA/Japanese consortium (Tsuneta at al. 1991). SXT allows for obtaining solar images in slightly different X-ray energy bands. The SXT images are recorded on the CCD detector. The point spread function of SXT depends on wavelength and the position relative to the optical axis within the image. Its shape is symmetrical only for the pixels located in the middle part of the CCD detector. A good analytical approximation of this function based on the results of pre-launch calibration was found by Martens, Lemen and Acton (1994). They have found that at least central part of the PSF can be described analytically in terms of the elliptical Moffat functions (Bendinelli, 1991) Nevertheless, existing analytical descriptions poorly reflect structural features of the PSF as wings extending far from the core of the function. In many SXT records, especially those with longer exposure times, the PSF wings may obscure large part of images, often reaching their boundaries and making any interpretation of the intensities very difficult; an example is shown in Fig 1.

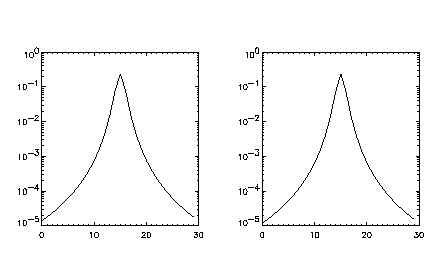
Figure 2: Analytical model of the Yohkoh SXT point spread function

DESCRIPTION OF THE METHOD

Our method bases on local properties of the images. It may be described in the following algorithmic way. First of all the entire image is being looked thoroughly for all local signal maxima exceeding certain threshold value. Next all local maxima found are inspected for any defects. Some of them, such as saturated points, single spikes are cast aside as these typically do not contain information about PSF blurring. Then for each of selected maxima the path of the steepest descent is determined and normalised by dividing the values of the pixels that lie on the path by the value of currently processed maximum. Such a path typically consists of several to several tens of points. All paths founded are inserted into a common array and "glued together topologically" in order to build a surface of elements with maximal slope in the image. After background subtraction and renormalisation, such a surface is considered as an approximation of the actual PSF. Renormalisation of the surface is necessary to ensure that the integral over its support equals unity. The method was tested on noisy images of simulated brightness distributions blurred by an analytical model of the PSF function. The method gave excellent results during the tests.

THE RESULTS

We show pictorially on two examples the restored PSF functions. The first restoration was made for solar flare image taken in SXT Be filter Fig 3. and Fig.4. The second one shows recovered PSF for SXT AlMg filter from SXT eclipse image Fig 5. and Fig.6.

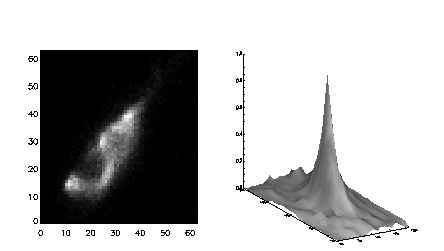
Figure 3: The result of PSF reconstruction (right) for an image of the solar flare from 20-Oct-95 taken in the SXT Be filter (left).

CONCLUSIONS

The first results of the presented method of recovering PSF functions for Yohkoh SXT telescope yield promising results. Obtained PSF shapes are irregular and asymmetric what may reflect the real SXT PSF structural features. Restored PSF profiles are more fuzzy than those approximated from analitycal models. At present, the method allows for determining, from the SXT data, the surface that is an upper close limit for the SXT PSF. The method however is in an early developmental stage and needs improvements, especially as concerns the maxima selection procedure, what may yield better PSF restoration results.

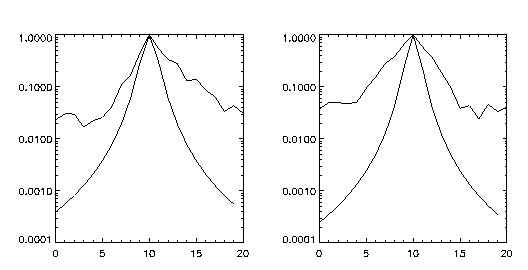
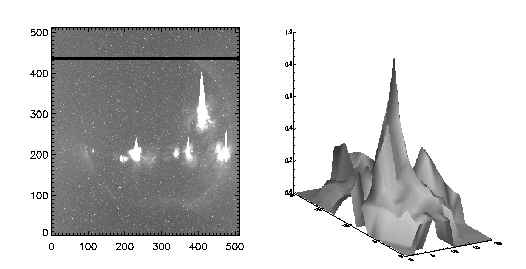
Figure 5: The result of the PSF reconstruction for an image of the solar eclipse (right) from 03-Nov-94 taken in the SXT AlMg filter (left).

References

Footnotes:

e-mail: sg@cbk.pan.wroc.pl

File translated from T_EX by T_TH, version 2.25.
On 05 Oct 1999, 16:45.